Logiciel de construction d’un matériau virtuel
Projet de fin d'étude
Résumé: L’objectif du projet est de réaliser un logiciel de construction de matériaux virtuels. Le matériau virtuel doit synthétiser toutes les caractéristiques importantes du matériau réel de manière à pouvoir ensuite être étudié par des séries d’expériences virtuelles. On doit pouvoir passer d’une description géométrique complexe d’une structure à sa représentation, ou à une de ses représentations en 3D, interactive et « interrogeable » par la souris.
SOMMAIRE
1.1 Présentation du laboratoire.
1.2. Présentation du contexte du projet.
2. Description du cahier des charges.
2.1. Construction du matériau virtuel.
2.2. Visualisation du matériau virtuel.
2.3. Extraction de données.
3. Description du travail effectué.
4. Planning du projet.
CONCLUSION
BIBLIOGRAPHIE
ANNNEXES
A. Diagramme de Voronoi et triangulation de Delaunay.
B. Algorithme de vérification qu’un point est à l’intérieur d’un volume.
Figure 1: Schéma générale de fonctionnement.
Figure 2: Description de divisions et de joints.
Figure 3: Hiérarchie de la structure d'une division.
2. Description du cahier des charges.
Le projet peut se diviser en 3 parties:
- Construction du matériau virtuel à partir de courbes statistiques.
- Visualisation du matériau virtuel.
- Extraction de données à partir du matériau virtuel construit.
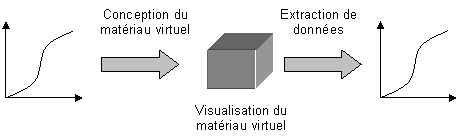
Figure 1: Schéma générale de fonctionnement
2.1. Construction du matériau virtuel.
Tout d’abord, un matériau (comme une division et les sous divisions de celui-ci) est composé d’un ensemble de plans, eux-mêmes composés de lignes, puis de points. Lors de la construction, le matériau peut être divisé en grains qui eux-mêmes peuvent être encore divisés en sous divisions. On aura ainsi plusieurs niveaux d’imbrications:
- Niveau 0: matériau.
- Niveau 1: grains.
- Niveau 2: cellules.
- Niveau 3: arrangement de dislocations.
- Niveau 4: arrangement des atomes.
Toutes les constructions d’un matériau virtuel se font à partir de courbes statistiques décrivant des propriétés géométriques mais aussi d’autres propriétés physiques. Le matériau virtuel est construit à partir de courbes statistiques sur la base des propriétés géométriques du matériau. Celles-ci doivent être obligatoirement fournies:
- Courbes statistiques sur la taille des grains. La taille correspond à la distance entre les 2 points d’un rayon coupant un grain. Pour le calcul de la distance, nous effectuerons un quadrillage de droites ayant un angle d’inclinaison et un écart entre elles. Pour que la taille des grains correspond le plus possible à la courbe, nous pouvons utiliser le calcul de la moyenne, de la variance, du « skewness » (degré de symétrie) et du « kurtosis » de la courbe. Dans un premier temps, seule la moyenne, puis la variance sera prise en compte, les autres moments de la courbe étant plus difficiles à prendre en compte.
- Courbes statistiques sur la forme des grains (rapport de forme = grand diamètre / petit diamètre).
- Proportion de phases, avec les compositions chimiques associées. Les phases sont des régions de l’espace qui ont des propriétés physiques différentes.
Les autres propriétés sont physiques et optionnelles. Elles seront définies par l’utilisateur en fournissant leur nom et la courbe statistique associée. Il faudra aussi indiquer si elles s’appliquent aux joints (plan inter-granulaire) ou aux grains. La distribution des valeurs des propriétés se fera toujours de la même façon, par tirage aléatoire de nombres compris entre 0 et 1 et en utilisant la courbe de probabilités cumulées fournie. Pour chaque propriété, la courbe statistique d’un matériau doit se rapprocher au maximum de la courbe statistique d’entrée. A titre d’exemple, les principales courbes seront:
- Courbes statistiques sur la disposition des atomes: plus spécifiquement sur l’orientation cristallographique du réseau des atomes, définie par 3 angles d’Euler (ou une matrice de rotation).
- Distribution spatiale des précipités et distribution de leur taille.
- Densité de dislocations.
- Fraction recristallisée et/ou taille des cellules de restauration.
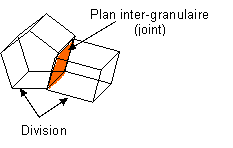
Figure 2: Description de divisions et de joints
Pour chaque courbe statistique, une propriété intervalle de probabilité peut être définie. Cette propriété indique que la partie de la courbe de l’intervalle doit être propagée aux divisions pour être utilisé lors de la sous divisions.
Toutes les propriétés doivent être hiérarchisées. Pour la visualisation à un niveau n, on ne doit pouvoir utiliser que les propriétés du niveau n (géométriques ou physiques), et celles des niveaux supérieurs (n+1, n+2…).
Toutes les sous divisions (par exemple: matériau en grains) sont construit avec l’algorithme de Voronoi. Mais, dans le futur, d’autres algorithmes doivent pouvoir facilement être ajoutés. En plus des informations de la structure géométriques du matériau, les points de Voronoï doivent être conserver pour effectuer des modifications sur le matériau lors des diverses itérations.
La construction des différents niveaux du matériau se fera l’un après l’autre. Un menu «construction» aura tous les niveaux d’un matériau et tant que celle précédant n’est pas construit, elles seront grisées. Si l’on choisit de construire un niveau, une boite de dialogue sera affiché permettant de paramétrer la construction en insérant les courbes sur les propriétés.
2.2. Visualisation du matériau virtuel
La visualisation permettra de manipuler le matériau (rotation, zoom, …) et voir les grains du matériau. Pour faciliter la visualisation des divisions, des coupes pourront être faites dans le matériau. Une sélection de divisions pourra aussi être faite, à partir de critères booléens (< = > …) sur les propriétés diverses. Seuls les divisions correspondantes à ces critères seront affichées.
Chaque division aura des propriétés, ainsi que chaque zone séparant 2 divisions (ces zones sont appelées joints de divisions). Ces propriétés seront accessibles après sélection d’un joint et seront définies grâce aux courbes statistiques données lors de la construction du matériau. Lors d’une sélection, il y a aussi interaction avec l’interface homme machine.
L’IHM (Interface Homme Machine) se composera de deux parties: la partie visualisation 3D et la partie navigation. Cette dernière partie sera un onglet composé de feuilles: grains, plans, points. Dans chacune de ces feuilles, on aura une hiérarchie indiquant les liens entre les grains, plans et points. Lors d’une sélection dans la hiérarchie, une boite de dialogue sera affiché avec les propriétés de l’objet. Lorsqu’un double-clique est effectué sur un joint dans la zone de visualisation, une boite de dialogue sera affiché avec toutes les propriétés ainsi que les divisions dont le joint appartient. En parallèle, dans la zone de navigation, le joint sera sélectionné.
La partie visualisation permet de voir seulement un niveau à la fois. Il sera donc possible de naviguer entre les différents niveaux. Pour visualiser une division (grain, cellules, …), il faudra sélectionner ce niveau.
2.3. Extraction de données
Des données sur le matériau construit pourront être extrait sous la forme de courbes statistiques:
- Taille des grains.
- Disposition des atomes, les orientations cristallographiques (angles d’Euler).
- L’ensemble des propriétés, géométriques ou non.
- Courbes statistiques sur les désorientations cristallographiques (entre grains).
- Etc.
On doit pouvoir extraire soit des courbes statistiques d’une propriété, soit la valeur particulière d’une propriété en une région de l’espace qui a été sélectionnée. Si les propriétés sont géométriques comme dans le cas de la sauvegarde de la structure du matériau, il faut fournir une liste hiérarchisée des divisions/plans/points qui constituent et permettent de représenter les objets concernés. Si les propriétés ne sont pas géométriques, il faut pouvoir dresser leur liste associée aux objets auxquels ils appartiennent qui, eux, ont une représentation géométrique.
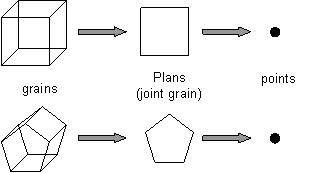
Figure 3: Hiérarchie de la structure d'une division